ADVERTISEMENTS:
The raindrop size, shape, mass, velocity, size distribution and its direction of fall are the main characteristics of raindrop.
These characteristics are described as below:
Characteristic # 1. Rain Drop Size:
The rain drop size has been evaluated by Lowe (1967), who caught several raindrops on a flat sheet of slate which was ruled into squares so that the size of splashes could be measured easily. This method of determining the size of raindrop based on the size of splash is one of the best methods.
ADVERTISEMENTS:
Another technique was also introduced which consists of an absorbent paper with light dust on its surface and a very finely powdered water-soluble dye. In dry condition the dye is invisible but on the exposure to rainfall, each raindrop makes an approximate circular stain on the absorbent paper which can be measured very easily.
The drop size can be calculated using the following formula:
D = asb
Where,
ADVERTISEMENTS:
D is the drop diameter,
s is the stain diameter, and
a and b are the constants, established by laboratory calibration for the absorbent paper used.
Hudson (1963) introduced another method for determining the size of raindrop known as Flour Pellet method. This method consists of catching the raindrops in a dish containing flour. When raindrop falls on the flour surface, then there forms small globules of wet flour.
ADVERTISEMENTS:
Several such wet globules of flour are formed during the rainfall, which are separated from each other; and are dried. The dried Hour globules are known as pellet. He also developed a calibration chart between the size of pellet and the size of raindrop, by which the average raindrop size can be obtained. This is most popular technique; and is widely used. The calibration chart is shown in Fig. 3.5.
Characteristic # 2. Terminal Velocity:
Rain is the liquid form of precipitation on the ground surface. And one of the components of the hydrologic cycle that begins from the water evaporation, formation of clouds in the atmosphere and ultimately falling on the ground surface. The water droplets falling from the cloud are the condensed water. The average size of raindrop is 6mm in diameter, i.e., the size of housefly. The falling velocity of raindrop depends on its size and weight.
The heavier the drop, the greater will be the falling speed. A large raindrop of about 5 mm size falls at the rate of 9 m/s (20 miles per hour). Drizzle which drop size is less than 0.5mm falls at the speed of 2 m/s (0.5 mph). When a raindrop falls to the ground surface, two forces, i.e., the gravity and drag forces act on it. A stationary raindrop initially experiences the force due to acceleration due to gravity 9.8 m/s2. The gravity force increases the speed of falling raindrop.
ADVERTISEMENTS:
The drag force retards the downward acceleration of raindrop. The air resistance that comes in contact with the water droplets as they fall, causes the drag force. The air resistance depends on the shape of raindrop, the cross-sectional area of drop and the speed of raindrop. In general, most of the raindrops are fairly round. The smaller drops are spherical, while larger drops are flat from the bottom because of airflow. At high speeds the air resistance varies as the square of the velocity.
From the cloud mass a falling raindrop picks up the speed because of gravity force. Simultaneously, the drag force of the surrounding air slows the drop’s speed. The two forces, i.e., the drag force and gravitational force becomes in balance mode, when air resistance becomes equal to the weight of the raindrop.
At this condition the drop attains an equilibrium speed, called terminal velocity. By terminal velocity the raindrop hits the ground surface. At terminal velocity stale the raindrop experiences no further acceleration; and therefore rain drops fall at a constant velocity. In brief, the rain drops attain terminal velocity when gravitational, drag and buoyant forces acting on the drop become in balanced form.
It can be presented by the following expression:
ADVERTISEMENTS:
mwg = mag + 1/2 v2 CD ρA …(3.19)
Where,
mw – mass of the drop
ma= mass of the displaced air
g = gravitational acceleration
v = velocity of the drop
CD = drag coefficient
ρ = density of air
A = reference area used in the drag-force equation.
In above equation, the parameters A and CD are not constant, are the functions of mass and velocity of the drop.
The values of terminal velocities of different types of rain are summarized in Tables 3.3 and 3.4.
Characteristic # 3. Shape of Raindrop:
The most important physical factors affecting the shape of raindrops are the surface tension, gravitational force, drag and buoyant forces. In case of very small drops (diameter 1 mm) the surface tension dominates; and constricts the drop to be into spherical shape, provided that the ratio of drop surface to its volume is minimum.
Since, surface tension is acting as energy per unit surface area, therefore, it becomes effective when surface area of rain drop is more. At bigger drop size the other factors also contribute few energy to the total energy of falling drop. In this condition, the shape of drop becomes flat at the bottom, and gradually gets break up due to pressure difference caused by greater drag-force than the surface tension forces.
Terminal velocity may be described as when a body falls under gravity force from few height then it accelerates until frictional resistance of the air is being equal to the gravitational force; and at this stage the body continues to fall with a constant velocity; this velocity is referred as terminal velocity. It depends on the size and shape of the falling body.
Fig. 3.4 shows the relationship between terminal velocity and rain drop size, which indicates that as the size of rain drop gets increase, the value of terminal velocity also increases, accordingly. For example, the largest drop of 5 mm diameter has a terminal velocity of about 9 m/s, while a rain drop of 1.5 mm size has terminal velocity about 4.5 m/s.
The velocity of falling raindrop can be computed by using the following equation given by Schmidt as:
In which, Vk is the velocity of falling rain drop (m/s) and d is the drop diameter (cm). The values of terminal velocities for different sizes of water droplets in stagnant air (pressure 101.3 kpa and temperature 20°C) are given in Table 3.6.
Chow et.al (1986) have reported the derivation of formula for terminal velocity of raindrops, based on the following forces acting on the falling raindrops:
1. Gravity force (Fg) – it is due to weight of raindrop.
2. Buoyancy force (Fb) – due to displacement of air by the rain drop.
3. Drag force (Fd) – due to friction between the rain drop and the surrounding air.
Let,
D is the drop diameter (assuming the shape of raindrop as spherical)
It is usually found that the raindrops up to 1 mm diameter are in spherical shape; beyond this size the drops become flattened from the bottom and oval in cross-section. In this condition the raindrops are characterized by equivalent diameter of sphere having same volume. The raindrops can range maximum up to 6 mm in diameter, but drops greater than 3 mm are uncommon, especially in low-intensity rainfalls.
Characteristic # 4. Drop Size Distribution:
It is the proportion of large and small size raindrops accomplished in a particular rain storm. It varies with the kinds of storm. It plays an important role on soil erosion, that how the drop size distribution affects the soil erosion in mass. From observations, it has been found that a low intensity rainfall mainly consists of small size drops in majority, while high intensity rainfalls from a thunder storm include greater proportion of bigger size rain drops. The drop size distribution can be studies by the methods of drop stain and flour-pellet methods.
An average drop size always provides best index of drop size distribution for a given storm. It is indicated by D50, which is the drop diameter such that 50% of the total rainfall includes small size raindrops and other 50% has bigger size raindrops.
Based on the plot of cumulative rainfall volume and drop diameter (Fig. 3.7), Best (1950) developed a relationship between D50 and the rainfall intensity (I) given as:
D50 = aIb …(3.28)
In which, a and b are the constants. This relationship is valid for low rainfall intensity, only. For study of drop size distribution of rain events of varying intensity, Hudson (1963) conducted an experiment and plotted the drop size distribution curves for low and medium and high rainfall intensities, as shown in Fig. 3.8 and 3.9 respectively. A curve was also developed by plotting the D50 and rainfall intensity (Fig. 3.10), which shows the relationship between D50 and rainfall intensity, as D50 ∝ I6.
Characteristic # 5. Momentum and Kinetic Energy:
From experimental evidence it has been found that the erosive power of rainfall is closely related to the kinetic energy and momentum of the rainfall. These two characteristics can be evaluated by making combinations of more than one physical properties of rainfall. For example, if the size of raindrops and their terminal velocities are known, then momentum and Kinetic Energy of falling raindrops may be obtained.
There is also an instrument known as “acoustic recorder” can be used for measurement of kinetic energy in form of sound. The working principle of this instrument is that, when a rain drop falls on its diaphragm, emits the sound which is calibrated in terms of KE of drop.





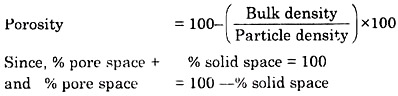
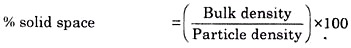






Comments are closed.