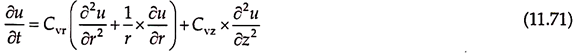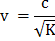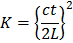Consolidation of Soil: Meaning and Mechanics, Types, Terzaghi’s Theory and Determination

In this article we will discuss about:- 1. Meaning of Consolidation 2. Mechanics of Consolidation 3. Types of Clay Deposits (Consolidated Clay) 4. Pre-Consolidation Pressure 5. Ultimate Consolidation Settlement 6. Secondary Consolidation 7. Terzaghi’s Theory 8. Determination of Coefficient.

Contents:

1. Meaning of Consolidation
2. Mechanics of Consolidation
3. Types of Clay Deposits (Consolidated Clay)
4. Pre-Consolidation Pressure in Soil
5. Ultimate Consolidation Settlement of Soil
6. Secondary Consolidation of Soil
7. Terzaghi’s Theory of Consolidation
8. Determination of Coefficient of Consolidation

1. Meaning of Consolidation:

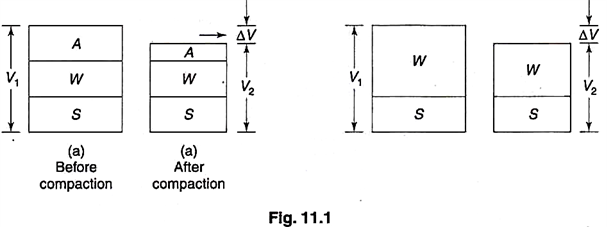
Consolidation is the gradual reduction in the volume of a partly or fully saturated soil under sustained loading and is mainly due to the expulsion of water from the soil pores.

When a static load is applied to a saturated (or nearly saturated) clay. It is first carried by the pore water because the structure must compress to take the load. There is a sudden increase in the pore water pressure, called the ‘excess pore pressure’ and its initial value v₀ is equal to the total, applied external pressure.

This build-up of excess pore pressure causes the water to drain out of the pores, allows the soil skeleton to compress and consequently get stressed. The excess pressure is thus gradually transferred from water to soil particles as effective pressure. Equilibrium occurs when all the excess pressure in water is transferred to soil skeleton as effective pressure and no more water drains out.

This process of expulsion of water from soil due to excess pore pressure with gradual reduction in soil volume accompanied by transfer of pressure from water to soil particles is called the ‘process of consolidation’.

The consolidation (as compression) of soil usually occurs in three stages:

1. Initial consolidation — It is a comparatively a sudden reduction in soil volume on application of the load mainly due to expulsion and compression of air present in soil pores.

2. Primary consolidation — It is the main phase of compression due to expulsion of pore water and dissipation of excess pore pressure. It is a time settlement phenomenon.

3. Secondary Consolidation — Even after dissipation of the excess pore pressure, some compression of soil continues at a gradually reducing rate which is known as secondary consolidation. It is a complex process and is thought to be due to the adjustment of internal structure of the soil.

---

ADVERTISEMENTS:

2. Mechanics of Consolidation:

The consolidation process of a saturated clay layer undergoes as under.

Immediately, on application of a pressure increment Δ_p, it is entirely taken up by the water in the pores, causing an excess pore pressure, also called hydrodynamic pressure (represented by say u̅). Thus at t = 0, u̅ = Δ_p. At this stage, the pressure transferred to the soil grains is nil.

If this transferred pressure is represented by ΔP̅, then when t = 0, ΔP̅ = 0. At any time afterwards, ΔP = u̅ + ΔP̅, and with increasing time, u̅ decreases and ΔP̅ increases, till finally u̅ becomes zero when the consolidation gets completed, and then ΔP̅ becomes equal to ΔP̅.

Figure 11.7 illustrates for a clay layer, which is being drained at both ends. In this case, at time t = 0 or t_∞ the excess hydrostatic pressure will immediately fall to zero at upper as well as at the lower ends, because it is permitting two way drainage.

In the middle of the layer, however, full extra hydrostatic pressure will prevail, i.e., equal to u. Rectangle ABCD thus represents the initial hydrostatic excess pressure diagram.

At any other time say t₁, t₂…, the excess pressure diagram will be somewhat triangular, as the pressure at the centre will go on reducing, till it becomes zero at t = ∞. The excess hydrostatic pressure diagram or isochrones corresponding to t₁, t₂… t_∞ would be as shown in Fig. 11.7.

The load transferred to the soil grains at any time, i.e., ΔP̅ can be worked out by subtracting the area of that curve from the total area ABCD. The ratio of this area to the area ABCD would eventually indicate the extent or the degree of consolidation at that time, and is usually expressed as percentage.

This degree of consolidation, U, at any time t after the start of consolidation process, can be expressed by the simple relation.

U = Δh/ΔH

Where Δh = compression at any time t.

ΔH = total ultimate compression

Alternatively, this can be expressed in terms of void ratio, as —

Where e₀ is the initial void ratio (at the start of consolidation), e_f is the final void ratio (at the end of consolidation) and e is the void ratio at any time t.

Practical Deduction:

The time taken by two soils (of different depths but with similar drainage) for achieving the same degree of consolidation are proportional to the square of their depths.

---

3. Types of Clay Deposits (Consolidated Clay):

In the natural process of deposition, fine-grained soils, like silt and clay undergo the process of consolidation under their own weight of overburden pressure. A state of equilibrium is reached after an elapse of several years and the compression ceases.

This process continues, season after season, and sometimes erosion or removal of overburden takes place, and sometimes the process of consolidation may continuously take place due to frequent deposition. So it is evident that clay soil deposits exist in the field under different conditions and their stress history should be known.

1. Normally Consolidated Clay:

If the present effective overburden pressure in the deposit is the maximum pressure to which the deposit has ever been consolidated at any time in the past, such a deposit is called a normally consolidated clay deposit. There is no reliable procedure available to predict the in situ effective stress-void ratio relationship.

A field e-p relationship has to be obtained from a carefully obtained undisturbed soil sample. Whatever the case with which the sampling operation is performed, there is bound to be some disturbance due to stress removal.

Accordingly, the shape of e – log p (or e – p) curve is strongly influenced depending on the degree of disturbance. Increase in the degree of disturbance flattens the curve considerably, but the straight line portion (in e-log p-curve) converges at a low void ratio as shown in Fig. 11.8.

Schmertmann (1955) assumed that the straight line portion of the laboratory and in situ curves coincide at 0.42 e₀. The in situ void ratio may be taken equal to the initial void ratio at the start of the test, without appreciable loss of accuracy. Further, for normally consolidated clays the pre-consolidation pressure (P_c) is equal to the effective overburden pressure (P₀). This is not the case in the deposits which are subjected to thixotropic, secondary compression or cementation effects.

Thus, in situ (or undisturbed) compression curve, called virgin curve, may be taken as line CD in Fig. 11.8 values of m_V or C_c have to be obtained from the virgin curve used in the computation of settlement. Terzaghi and Peck based on Skempton’s earlier concept, proposed an empirical equation for C_c as C_c = 0.009 (W_e – 10%).

Suggest C_c = 0.30 (e₀ – 0.27).

2. Over-Consolidated Clay:

A clay soil deposit that has been fully consolidated under a pressure P_c in the past, larger than the present overburden pressure P₀, is called an over-consolidated (pre-consolidated or pre-compressed) clay deposit. The ratio (P_c – P₀)/P₀ is called the over-consolidation ratio (OCR).

Over-consolidation of clay may be caused by any or a combination of the following loads:

(i) Pressures due to overburden which have been removed (e.g., due to erosion or due to removal of an old structure)

(ii) Glacial ice sheets have since disappeared

(iii) Sustained seepage forces

(iv) Tectonic forces caused due to movements in earth’s crust

(v) Fluctuation of water table.

The in situ e-ρ relationship is radically changed by over-consolidation. Factors other than pressure which may affect the in situ e-ρ relationship are weathering, deposition of cementation materials and leaching of ions from the pore water.

The in situ e-log P curve is obtained following the procedure given below and as shown in Fig. 11.9.

(i) Consolidation tests are performed on undisturbed samples and loading, unloading and reloading are continued till a reasonable straight-line portion of the e-log P-curve is obtained.

(ii) The pre-consolidation pressure P_c is estimated.

(iii) A line from the point G (e₀, P₀) is drawn parallel to the mean slope of the rebound curve.

(iv) Select a point G’ on this line corresponding to P_c. From this point, a line is drawn to meet the point (F) of intersection of the laboratory curve at 0.42 e₀.

(v) The dot-dashed lines GG’ and G’F are then used to obtain C_c for calculating the settlement.

3. Under-Consolidated Clay:

Rapid natural deposition or deposits under recent fillings may not be fully consolidated under the present overburden pressure; such clay deposit is called under-consolidated clay (Fig. 11.10).

In such cases P_c < P₀ and structures constructed on this deposit will cause additional compression. No specific procedure is available to get in situ e-p curve. However, for all practical purposes this may be treated as normally consolidated for the purpose of calculating settlement.

---

4. Pre-Consolidation Pressure in Soil:

The maximum pressure to which an over-consolidated soil had been subjected in the past is known as the pre-consolidation pressure or over-consolidation pressure (P̅_c). When a soil specimen is taken from a natural deposit, the weight of the overlying material (overburden) is removed. This causes an expansion of the soil due to reduction in pressure.

Thus, the specimen is generally pre-consolidated or over-consolidated when the specimen is loaded in the consolidation test, the initial portion AB of the compression curve ABCD is actually a recompression curve. Consequently, the initial portion AB is relatively flat. It is followed by a straight line CD with a steep slope which indicates the compression of a virgin (normally consolidated) soil.

In the transition range BC, the slope gradually changes. The pre-consolidation pressure (P̅_c) falls in this range.

Casagrande Method:

1. Determine the point E on the curve where the curvature is maximum, i.e., the radius of curvature is minimum. (Fig. 11.11)

2. Draw the tangent EF to the curve at E.

3. Draw a horizontal line EG at E.

4. Bisect the angle between the tangent EF and the horizontal EG, and draw the bisector EH.

5. Produce back the straight line CD of the curve and determine the point of intersection P of the bisector EH and the backward extension of CD.

6. Draw the vertical PJ through P which cuts the log P̅ axis at J. The point J indicates the pre-consolidation pressure P̅_c.

---

5. Ultimate Consolidation Settlement of Soil:

Two types of settlements, viz., immediate settlement and time-dependent settlement. The time dependent settlement may be divided into settlement due to consolidation and settlement due to secondary compression or creep.

Hence, the total settlement (S) of any soil mass under an applied stress is given-

S = S_i + S_c + S_s

Depending on the type of soil each component gets its importance. For coarse-grained soils S_i predominates. In fine grained soils S_c predominates, and in organic soils S_s has a vital role to play. Consolidation theory is usually used for the prediction of settlement in saturated fine grained soils.

Creep – Time dependent deformation or slow movement of soil debris.

Settlement in Terms of C_c (Compression Index):

Δe = e₀ – e = A constant X(log P – log P₀)

where e₀ and P₀ are the initial void ratio and pressure, and e is the void ratio attained at pressure P. The constant is called the compression index (C_c).

Compression Index:

---

6. Secondary Consolidation of Soil:

The settlement continuing beyond primary consolidation is known as secondary consolidation. Settlement due to secondary consolidation is usually very small in inorganic soil.

The slope of the secondary branch of the settlement versus log time curve is termed secondary compression index C_∝ and is used for computing secondary settlement as shown in Fig. 11.16.

Because of the existence of a plastic lag right from the beginning of loading, secondary consolidation is believed to come into play, though its magnitude is small. This is also the reason why the experimental time-consolidation curve is in agreement with Terzaghi’s theoretical curve only upto about 60% consolidation.

The contribution of the secondary consolidation to the final settlement varies with the type of soil. For most of the mineral soils, secondary consolidation is small and can be neglected. In case of organic soils, micaceous soils, loosely deposited clay, etc., secondary condition may constitute a substantial part of the total settlement.

---

7. Terzaghi’s Theory of Consolidation:

In order to compute the amount of consolidation (or say settlement) after any given time t, Terzaghi evolved this theory, which considers the very fact that the “consolidation is directly based upon the expulsion of pore water”.

For a soil cube, considering such pore water flow.

Let us, therefore, consider a soil cube. We will also consider, only one-dimensional theory, by assuming that water is flowing through this cube only in one direction (say vertical—z-axis). Now, the quantity of water flowing into the cube in time dt.

Various assumptions have been made:

(a) The soil mass is homogeneous.

(b) The void spaces are completely filled with water.

(c) The soil solids and water are incompressible.

(d) Darcy’s law is valid.

(e) The seepage flow and deformation are in one-dimensional direction.

(f) Strains are small.

(g) The permeability is constant over the range of effective stresses.

(h) This is a unique pressure – void ratio relationship, i.e., the coefficient of compressibility is constant.

(i) The time lag in consolidation is entirely due to the low permeability of the soil.

Application of Terzaghi’s Consolidation Equation:

---

8. Determination of Coefficient of Consolidation:

By applying a series of load increments to the soil sample and recording settlements at selected time intervals, the consolidation test proceeds. Observations of compression versus time for each load interval are taken and the data are plotted on either a semi-logarithmic plot or square root of time. The purpose of these plots is to obtain the values of t₅₀ (time at 50 per cent consolidation) and t₉₀ respectively.

The value of t₅₀ is obtained by carrying out following steps from a semi-logarithmic plot:

(i) Select a time t₁ in the initial portion of the curve which is parabolic.

(ii) Select a second time t₂ = 4t₁ in this parabolic portion of the curve.

(iii) Obtain the offset between t₁and t₂

(iv) Plot this offset distance above t₁ to obtain R₀.

(v) R₁₀₀ value is obtained by the intersection of tangents drawn to the mid-curve area and the end portion (Fig. 11.14).

(vi) R₅₀ is then taken as (R₀ + R₁₀₀) / 2 and the time corresponding to this is t₅₀.

From square root of time plot, value of t₉₀ is obtained as follows (Fig. 11.15).

(i) The straight line obtained by joining the initial points is extended to abscissa and a point 15 per cent larger is located. This straight portion is produced backward to intersect the ordinate at R₀, which is the corrected zero reading corresponding to U = 0.

(ii) Joining points R₀ and B, a second straight line drawn.

(iii) The point of intersection of the second straight line and the original curve locates R₉₀ and the corresponding time is t₉₀.

The t₅₀ and t₉₀ values are used to compute the coefficient of consolidation C_v which is given by –

C_V = (T_v x H²)/t_i

Where,

T_v = time factor

H = length of drainage path (it is half when drainage is from both faces)

t_i = time for i per cent consolidation

The value of time factor depends as degree of consolidation, U and is given as under for linear pore pressure distribution –