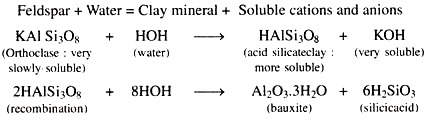
ADVERTISEMENTS:
Some of the common methods for calculating Hydraulic Conductivity are described below:
Hydraulic conductivity is the coefficient k in the Darcy’s law v = ki, where v is the velocity and i the hydraulic gradient. Hydraulic conductivity values can be determined in the laboratory using disturbed soil samples.
As laboratory values are determined using disturbed samples, they do not exactly tally with field values. In drainage practice, field methods for determining hydraulic conductivity are widely used.
1. Single Auger Hole Method:
ADVERTISEMENTS:
This method is used when the watertable is present near the ground surface. This methods consists of drilling a hole extending into the watertable. A casing pipe is installed to prevent the sides collapsing into the bore.
Water is removed quickly from the bore either by using a pump or more conveniently using a bailer.
The rate of rise of water in the bore is measured and using these measurements the hydraulic conductivity of the soil is calculated as explained below:
Hooghoudt’s Equation:
ADVERTISEMENTS:
The equation used for calculating the hydraulic conductivity was derived by Hooghoudt and is known as the Hooghoudt’s equation. Fig. 18.5 indicates the different terms involved in this equation.
The assumptions in deriving the equation are as follows:
1. The watertable around the auger hole is not lowered when water is removed from it. This condition is satisfied for a short while after the auger hole has been pumped. This condition will not be valid if the auger hole is repeatedly pumped.
ADVERTISEMENTS:
2. Water flows horizontally into the sides of the auger hole arid vertically up through the bottom of the hole.
Using the second assumption, it can be taken that the rate at which the auger hole is filled is
directly proportioned to the circumference of the hole and is inversely proportional to the cross sectional area of the hole. The rate of rise of water in the hole at time t is now written as – 
Because in the experimental conditions a finite size sandtank has been used, S is only an approximation to the field value. Hooghoudt states that the above equation is accurate to within 27 per cent of the true value.
ADVERTISEMENTS:
This accuracy he considers adequate for the determination of the hydraulic conductivity considering the fact that the K values in the field varies 0.001 to more than 10 m/day. The coefficient 0.19 in the above equation has dimension of L and is valid for metres only.
As water flows upward through the bottom of the auger hole, the rate of rise of water in it can also be written as –
2. The Pipe Cavity Method:
This method proposed by Kirkham (1946) consists of driving a pipe or tube into the soil and below the watertable. Soil is augered out of the pipe. After the water comes into equilibrium, it is pumped out several times in order to remove puddled soil from the walls of the cavity. This is checked by the consistency of the conductivity values obtained in the individual pipe. Water is pumped out and the rate and rise of water in the pipe is measured.
ADVERTISEMENTS:
Kirkham developed the following formula for determining the conductivity –
Notations used in the above equation are given in Fig. 18.6. S is a coefficient known as shape factor; Values of S are determined using electric analogue experiments. Fig. 18.7 shows the value of S/a for different values of L/a.
3. Cylinder Permeameter Method:
This method is essentially carrying out the laboratory method of determining permeability in field conditions. In this method a fairly large diameter hole is dug to the desired depth. A steel cylinder with a diameter of 50 cm is placed in the centre and driven into the ground to a depth of about 15 cm.
Two tensiometers are installed in the annular space between the steel cylinder and hole, on opposite sides and at a depth of about 20 cm. Water is ponded in the steel cylinder and in the hole to equal depth (15 cm).
When the tensiometers indicate zero pressure head, saturated flow through the cylinder is assumed. The rate of flow is noted and using Darcy’s law, the hydraulic conductivity is calculated.
This test gives the hydraulic conductivity of the soil in the vertical direction.
4. Pond-Infiltration Test:
This method is a quick field method of finding the hydraulic conductivity. This essentially gives the vertical hydraulic conductivity. The procedure consists of forming a circular pond with a dike around and 400 cm in diameter. A circular shape is recommended than a rectangular one.
Water is added to the pond till sufficient depth of the soil is fully soaked. Water is ponded and the rate of fall of water is noted. Since the flow is almost entirely due to gravity, the hydraulic gradient will be unity and the hydraulic conductivity is calculated using Darcy’s law as mentioned in the previous method.
5. Hydraulic Conductivity of Layered Soils:
When the soil profile consists of two layers with appreciable difference in hydraulic conductivity, the auger hole method can be used for determining the hydraulic conductivity of each of these layers in the following manner.
The method is due to Earnest and it assumes that-
(1) The flow lines are horizontal and independent in each layer, and
(2) The amount of water flowing in each layer is dependent only on the hydraulic conductivity of that layer.
Even though both these assumptions are not fully valid, the error due to these assumptions, as indicated by Earnest is of the order of 10 per cent.
The procedure consists in digging two auger holes (Fig. 18.8) one in the first layer, the bottom of the hole being 10 cm above the interface. The second hole should extent well into the second layer. For two layer system, Earnest derives the equation –
Where, K is the mean value of the conductivity as determined in the second hole, K1 and K2 are the conductivities of the first and second layers respectively.
After determining the conductivity of the first layer and the mean conductivity using the second auger hole. Using the above formula, the conductivity of the second layer can be calculated. An accurate value of the conductivity of the second layer can be obtained when the watertable level is within the second layer itself.