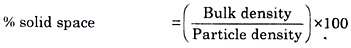ADVERTISEMENTS:
After reading this article you will learn about estimating the volume of runoff.
Knowledge of the volume of runoff from a watershed is necessary to design the water storage system and surplussing arrangements. Different mathematical models that are developed to predict runoff deal mainly with precipitation characteristics affecting runoff amount and peak rates.
In an attempt to simplify and standardize runoff prediction, the soil conservation service (SCS) of the United States Department of Agriculture (USDA) has developed a runoff prediction model, based on many years of storm flow records from agricultural watershed, and certain watershed characteristics, such as indices of the soil cover complex and antecedent moisture condition.
ADVERTISEMENTS:
Four hydrological soil groups have been recognised based on effective soil depth, clay content, infiltration rates and permeability characteristics of soils (Table 3.9). The four classes, listed A (the lowest runoff potential) through D (the highest runoff potential) include commonly occurring soil series in India.
(A) Low Runoff Potential:
Includes deep sands with very little silt and clay, also deep, rapidly permeable loess, Infiltration rates may be more than 25 mm/hr.
ADVERTISEMENTS:
(B) Moderately Low Runoff Potential:
Includes mostly sandy soils, less deep than A and less aggregated than A, but has above average infiltration rate (12.5 – 25.0 mm/hr) after thorough wetting.
(C) Moderately High Runoff Potential:
Includes shallow soils, containing considerable clay and colloids. Below average infiltration rate (2.5 to 12.5 mm/hr) after pre-saturation.
ADVERTISEMENTS:
(D) Highest Runoff Potential:
Includes mostly clays of high swelling percentage. The group also includes some shallow soils with nearly impermeable sub-horizons near the surface. Infiltration rate may be less than 2.5 mm/hr. Vegetation has a key role in determining runoff. Depending upon cover and land use pattern the following hydrologic conditions have been described for forest and tree crops.
Watershed characteristics are described in terms of land use, cropping practice, hydrologic condition and hydrologic soil groups. Land use may vary from row crops to roads with most of the divisions associated with various agricultural uses.
ADVERTISEMENTS:
Treatment classes consist of straight row cropping, contouring and terracing. The land use and treatments on an area are further divided into three hydrologic conditions viz., poor, fair and good. These characteristics of the watershed are quantified in terms of runoff curve numbers as shown in Table 3.10a, b.
Antecedent moisture is also an important factor in determining the runoff. It is defined as the summation of the 5 day precipitation before the runoff- producing storm, and is called antecedent moisture condition (AMC) I, II, III. These conditions are defined both for dormant and growing seasons (Table 3.11).
Curve numbers for the three AMC conditions are inter-convertible using suitable correction factor (Table 3.12).
Initial abstraction of rainfall, before runoff begins, is also an important factor determining the actual runoff. The initial abstraction consists of interception losses, surface storage, and water which infiltrates into the soil prior to runoff. The value of Ia is assigned from the general condition of the region.
For example:
(a) Black soils region AMC II and III – Ia = 0.15
(b) Black soils region AMC I – Ia = 0.3 S
(c) For all other regions – Ia = 0.3 S
where, Ia is the initial abstractions over the catchment before runoff begins, expressed in equivalent depth of water, and S is the potential maximum retention or infiltration (difference between rainfall and runoff).
Knowing these watershed conditions, hydrologic soil-cover complexes and antecedent moisture, through the use of appropriate tables and graphs, one can determine the appropriate curve number.
With the curve number, runoff can be predicted for a given watershed rainfall using the relations (SCS, USD A):
Q = (I’ – 0.2S)2/(I’ + 0.8S) …(3.10)
where, Q = direct runoff,
I’ = storm rainfall.
In Eq. (3.10) the initial abstraction la has been considered to be 0.2 S. For convenience in evaluating antecedent moisture, soil conditions,’ land use and conservation practices, the U.S. soil conservation service defines.
S = 1000/N – 10 …(3.11)
where, N = an arbitrary curve number ranging from 0 to 100. For N = 100, S = 0 and, therefore, I’ = Q.
Curve numbers can be obtained from Table 3.10a. On gaged watersheds S can be obtained directly from the plot of actual rainfall (I’) and runoff (Q) data as shown in Figs. 3.6 and 3.7.
Q = (I’ – 0.3S)2/(I’ + 0.7S) …(3.12)
Q = (I’ – 0.1S)2/(I’ + 0.9S) …(3.13)
Equation (3.12) is applicable to all soil regions of India except the black soil areas for which Eq. (3.13) is most appropriate.
The arbitrary curve number N for different soil conditions can be obtained from the relation:
N = 25400/254 + S
The U.S. soil conservation service staff have also suggested 6 hours as the minimum storm period for flood-water-retarding structures. For determining I’, therefore, charts for 6 hours rainfall for 10,25 and 50 years frequency (Figs. 3.8, 3.9, 3.10) have been developed for various geographic locations of India.
From rainfall-retention relationships, following equation was developed by Wasiullah and Ram Babu (1970) for estimating runoff volume:
Q = 0.14 A0.3 q …(3.14)
where, Q = volume of runoff, ha m
A = Area of watershed, ha
q = peak discharge, cumec