ADVERTISEMENTS:
In this article we will discuss about:- 1. Sediment Transport 2. Sediment Load 3. Practical Aspects of Bed Formation 4. Tractive Force Theory 5. Effect of Side Slopes 6. Design of Channels in Coarse Alluvium 7. Estimation of Suspended Load 8. Estimation of Bed Load 9. Certain Formulae for Bed Load Transport 10. Einstein’s Formula for Bed Load Transport.
Contents:
- Sediment Transport
- Sediment Load
- Practical Aspects of Bed Formation
- Tractive Force Theory
- Effect of Side Slopes
- Design of Channels in Coarse Alluvium
- Estimation of Suspended Load
- Estimation of Bed Load
- Certain Formulae for Bed Load Transport
- Einstein’s Formula for Bed Load Transport
1. Sediment Transport:
ADVERTISEMENTS:
A flowing water in a channel, always tries to scour its surface. Silt, gravel or even larger boulders are first detached from its bed or banks, and then swept D/S by moving water. The phenomenon of detaching and then sweeping the silt or gravel from bed or banks is known is sediment transport. The phenomenon is of great economic importance.
Following are some of the important works where sediment transport has its effects:
1. The design and execution of flood control schemes is chiefly governed by the peak flood level, which in turn depends upon the scour and deposition of sediment.
2. Silting of channels and reservoirs also depends upon the sediment transport.
ADVERTISEMENTS:
3. Sediment deposited in rivers and harbours requires costly dredging.
2. Sediment Load
:
The quantity of solids (silt) entering the channel, is known as sediment load. It is a single important factor which controls the shape and cross-section of the true regime channel.
The sediment moving in a fluid can be broadly divided into two parts:
ADVERTISEMENTS:
1. Bed Load:
It is the load of bed material, in the bottom most layer of the flow. Suspension of sediment is not possible in this layer, because, of fluid dynamic reasons. The grains of bed load are not supported vertically by the flow but rest on the bed while rolling, sliding and jumping. The weight of the bed load particles is borne by the stationary grain particles of non-moving bed. The particles of bed load move regularly and exchange places with the similar particles of non-moving bed.
2. Suspended Load:
With increase in the velocity, smaller particles are thrown in suspension by the upward component of the turbulent velocity of flow. The particles always settle due to gravity effect. The flowing water provides an upward motion due to turbulent exchange. Due to turbulent exchange the water is regularly exchanged between various horizontal layers of water over a definite distance.
ADVERTISEMENTS:
The ascending water originates from lower layers of higher concentration and descending water originates from higher layer of lower sediment concentration. In this process of exchange of turbulences, there is a net upward surplus force, which provides an upward motion to sediment particles and counterbalances the settlement effect of the particles due to gravity. Suspended load also causes additional hydrostatic pressure on the bed of the channel.
3. Practical Aspects of Bed Formation
:
The bed of the channel in which water is flowing, may adopt various shapes depending upon the velocity of flow.
At very low velocity of flow, bed of the channel does not move at all. When velocity is slowly increased a stage is reached when the sediment load is just at the point of motion. This stage is known as “threshold of motion”. If bed is made of fine sand, having particles of less than 2 mm diameter saw tooth type ripples develop in the bed on slightly further increasing the velocity.
ADVERTISEMENTS:
This phenomenon can be easily seen in sand at beaches. At still larger velocity, dunes with ripples appear at the bed, which on further increase on the velocity take the shape of rounded dunes. When velocity is still further increased, the dunes are eliminated and a flat surface becomes available.
If velocity is increased still further, sand waves are formed in association with surface waves. When velocity is still further increased. Froude number (V/√gD) surface waves become so steep that they break and the whole wave system gradually moves upwards. The sand waves at this point of velocity are known as anti-nodes. Antinodes can form only in open channel flows and not in windblown sand, because they require an interaction between the bed of the channel and the water surface for their formation. See Figs 18.1 and 18.2.
4. Tractive Force Theory
:
In the study of mechanics of sediment transport, the soil particles are always considered as incoherent. Most of the river beds are made up of sand and gravel and as such assumption in regard to soil being incoherent is correct. The basic mechanism that controls the sediment transport, is the drag force exerted by water in the direction of flow on the channel bed. This drag force is also known as tractive force or shear force. This force is nothing but a pull of water on the wetted area of the channel.
Consider a channel of length L and cross-sectional area A. The volume of water in this length of channel would be A x L. If w is the unit weight of water, then weight of water stored in this length (L) of the channel will be ωAL.
Weight of water acting in vertical direction = ωAL. Horizontal component of this weight = ωAL sin θ. But θ is slope of the channel which is represented by S.
∴ Horizontal component of weight = ωALS.
Hence average unit tractive force also known as shear stress is given by τ = ωSR.
Where ω = Unit of weight of water
S = Longitudinal slope of the channel
R = Hydraulic mean depth H.M.D. (A/P)
In the case of wide open channels, the value of hydraulic mean depth (H.M.D.) is almost equal to depth of the channel. Hence tractive force can be written as follows also
τ = ωSD (2)
If tractive force becomes greater than the frictional resistance between particles, the particles are set in motion. The resistance of sediment to motion in proportional to the diameter d of the particle and the submerged weight of sediment in water.
The value of critical tractive force τ c becomes as follows:
τ c = C(G -1 )d
Where τ c = critical tractive force
C = constant (later it was also found to vary)
G = S.G. of the solid sediment particles
E.W. Lane gave following equation for critical tractive force τ c –
τ c (in kg/m2) = 0.078 d, where d is in mm.
Values of critical tractive force in kg/m2 for different soils are given in Table 18.1.
5. Effect of Side Slopes:
The stability of horizontal bed of the canal and developed equation τ = ωSD or ωSR where τ is the tractive or disturbing force. But on the slope of the banks there is one more disturbing force i.e. the component of the weight of the particle.
Consider a particle of weight w resting on the slope of the bank.
This particle is subjected to following forces:
(i) τ = ωSR.
(ii) Component of ωs along the slope of the bank ω sin θ.
(iii) Component of ωs normal to the slope of the bank R tan θ.
Where θ = angle of slope of the bank with the horizontal.
φ = angle of repose.
The various forces acting on the particle and their free body diagram are shown in Fig. 18.4.
τ c = W x µ = W tan φ
τ c is the critical shear stress that is required to move a similar grain on a horizontal bed.
Considering the free body diagram
This equation shows that τ c is greater than τ 0 which means that tractive force or shear stress required to move a grain on the slope is less than that required to move the grain on horizontal bed.
On the horizontal bed, average value of shear stress or tractive force, that will be generated by the flowing water in a channel is given by τ 0 = ωRS, while on banks it has been established to be
τc = 0.75 τ0 = 0.75 ωRS.
Shear stress or tractive force distribution is shown in Fig. 18.7.
The distribution of unit tractive force or shear stress is rectangular for bottom and parabolic for banks as shown in Fig. 18.7.
The value of unit tractive force (shear stress) also depends on the curvature of the canal.
Permissible tractive force for curved and straight canals are given as follows:
6. Design of Channels in Coarse Alluvium
:
Design of channel in coarse alluvium is done by Shield’s entrainment method.
This method has been explained as follows:
According to him the motion of a bed particle is dependent upon the following variables
τ0 = The shear stress or unit tractive force of the base.
Ps = Density of the grain or particle.
Ps = Density of fluid.
Pf = Diameter of particles.
d = Acceleration due to gravity.
µ = The dynamic viscocity of the fluid.
Out of all these variables, the shear stress (τ 0) is the most important factor as it measures the power of the flow that dislodges the sediment. This factor depends upon the velocity (V) of flow.
In order to study the movement of the bed particle, dimensionless method of analysis is adopted.
All the six variables listed above can be grouped to form three dimensionless numbers. The numbers are –
Although velocity term is not required, yet it is convenient to have a parameter with the dimension of velocity. We introduce a new term known as shear friction velocity and denote it by ‘V’.
Where is the kinematic viscosity of the fluid.
Combining (i) and (ii) dimensionless numbers, we get another dimensionless number as V’2/ gd (Ss-1)
It can be further simplified as follows:
Pfg = ω = Unit weight of water.
Ss = Specific gravity of the grain.
This number is known as Shield’s Entrainment function and is denoted by Fs .
![]()
The third dimensionless number which dV’ / V is known as Particle Reynold’s number Re where V is the kinematic viscosity.
Now we can easily say that motion of a particle is dependent upon these two numbers i.e. Fs and Re.
Graphs may be plotted between Fs and Re as shown in Fig. 18.8. The curve obtained forms the basis for the design of channels, where it is desired to prevent bed movement or to keep it to a minimum. At Reynold number 400 and above the value of Fs, becomes constant and thus application of this aspect becomes more simple and equal to 0.056. It has been seen that when particle size exceeds 6 mm diameter. Particle Reynold number has been found to be above 400.
Hence for channel in coarse alluvium (above 6 mm)
This equation gives the maximum size of the particle that will remain at rest in a channel of given R and S. If d is less than this the particle will set in motion.
Since with passage of time the smaller particles are flushed out of the surface, lined with coarse stones, actual size to be adopted should be somewhat larger than what is calculated from the equation d = 11 RS.
7. Estimation of Suspended Load
:
Suspended load of the channel can be estimated either by stream sampling or by the analytical method. Suspended load samplers may be used to measures the suspended load in the flowing water. Following equation is used to evaluate suspended load
Where is C =Sediment concentration at a height y above the bottom which to be determined by the above equation.
Ca = Known concentration at a known height a above the bottom of the channel.
f = Fall velocity of the grain in still water.
D = Depth of water.
K = Von Karman’s constant whose value is 0.4.
V’ = Shear friction velocity =
Where τ0 = Intensity of shear stress or tractive force at the bottom of the channel.
The above equation is known as suspended load equation. The limitation of this equation is that, it cannot be used directly to predict the sedimentation concentration at any point, unless, the sediment concentration at some known distance is pre-known.
8. Estimation of Bed Load
:
The most important factor responsible for the movement of the bed grains is the tractive force or drag force,
τ0 = ωRS
Where ω = Unit weight of water = 100 kg/ m3.
We also know that certain minimum value of shear stress or unit tractive force is required to move the grain, depending upon the internal friction of the soil particles. This force is called critical shear stress and is represented by c. For normal turbulent flow and for quartz grains, the value of c, has been estimated as c = 0.07 d where c is in kg/m2 and d is in mm.
When the unit tractive force caused by the flowing water ( 0) exceeds the critical unit tractive force ( c), the sediment starts moving. The rate of bed load transported must therefore be a function of ( 0 – f). But the problem becomes complex when we take into account the fact that as soon as the grain starts moving, the channel bed develops ripples and a large part of shearing force is absorbed in the form resistance caused by these ripples.
A part of the tractive force is therefore lost in overcoming the ripples and does not play any role in transporting bed material. The amount of shear stress lost in this process is not known and no perfect mathematical solution has been put forward to work out this quantity.
It has been widely accepted that the tractive force is reduced, due to ripples in following ratio:
Where ’0 = Unit tractive force left after the ripple resistance is overcome. It may also be stated as 0 minus tractive fore lost in overcoming ripples.
0 = ωRS, or original tractive force exerted by flowing water.
N’ = Rugosity coefficient that should come into play theoretically in a channel of given R and S. Its value may be obtained by Strickler’s formula
N’ = d1/6/24 where d is the effective grain size in metres.
N = Rugosity coefficient actually observed by experiments on the rippled bed of the channel and its value is generally taken as 0.02 for discharges over 11 cumecs and 0.0225 for smaller discharges.
R’ is the corresponding H.M.D. that would exist in the channel if the bed were un-rippled. In other words if we use the value of R’ in all our calculations, instead of R, we can forget about bed ripples i.e. the effect of ripples is only to reduce the hydraulic mean depth to a value R’ from R.
9. Certain Formulae for Bed Load Transport
:
Some formulae suggested by various investigators in regard to bed load transport are given here:
1. Du-Boy’s Formula:
qs = Cs 0 (0 – c)
Where qs = Volume of bed load transported per second per unit width of the channel.
0 = Average shear stress on the channel boundary.
c = Minimum shear stress required to move the particle, called the critical shear stress.
Cs = A constant which depends upon the grain size and is related to it by following relationship –
Here d is in mm but all other elements qs, c, 0 are in F.P.S. units.
2. Shield’s Formula:
Where S = Bed slope.
Ss = Specific gravity of the stone or grain.
q = Discharge per unit width.
ω = Unit weight of water.
d = Diameter of stone or grain.
3. Meyer-Peters Formula:
Meyer and Peter had suggested that the unit tractive force causing bed load to move, is reduced by ripples in the ratio of
The effective unit tractive force going to cause bed load transportation, is then given by –
On these concepts, Meyer and Peter had suggested the following formulae for calculating quantity of bed load transport –
Where gs is the rate of bed load transport (by wt) in kg/m per hour i.e. gs = gs ω Ss.
Where gs = Volume of sediment transported per meter width of channel per hour.
ω = Unit weight of water.
Ss = S.G. of the grain.
N’ = Manning’s coefficient pertaining to grain size on an un-rippled bed and given by Strickler’s, formula, N’= d1/6/ 24 when d is in meters
N = Rugosity coefficient actually observed on rippled channels. Its value is taken as 0.02 for discharges of more than 11 cumecs and 0.0225 for lower discharges.
v = Critical shear stress required to move the grain and given by c = 0.07 d where c is in kg/ m2 and d in mm.
0 = Unit tractive force produced by the flowing water i.e. ωRS. Truly speaking, its value should be taken as the unit tractive force produced by flowing water on bed i.e. 0.97 ωRS.
10. Einstein’s Formula
for Bed Load Transport:
Einstein’s formula for bed load transport is based on the principle of probability. It is a semi-theoretical approach to the problem of bed load transport. He assumed a number of elements and also a number of experimental coefficients.
The formula given by him correlates two dimensionless parameters φ and Ψ as follows:
Where φ = Einstein’s bed load function
Ψ = Fs = Shield’s entrainment function
qs = Volume of sediment transported per second per unit width
f = Fall velocity
d = Diameter of grain
φ and Ψ relationship is represented by a curve shown in Fig. 18.9. This curve can be used to design stable channels for a given bed load transport.
The straight line portion of the curve follows the relation
φ = 40 (Ψ)3.
Putting value of φ and Ψ we get
Now if it is assumed that channel is wide and Chezy’s C is constant then
This equation is an important form of Einstein equation. It shows that sediment carrying capacity of the channel depend upon the discharge per unit width.
Following important conditions can be drawn from this equation:
(i) With increase in width, the discharge per unit width (q) decreases (Q remaining constant) and thus qs / q i.e. sediment carrying capacity will reduce and deposition of sediment will start which will increase the bed slope. The silting will continue till the slope S is increased to such a value that qS2 becomes constant.
(ii) Since the sediment carrying capacity depends upon the discharge, the floods will carry more sediment. Floods are in fact mainly responsible for most of the annual sediment load. (iii) When branch channel is taken out from the main channel sediment carrying capacity of the main channel immediately D/S of takeoff point is reduced, because discharge per unit width (q) is reduced. This process would divert more and more of water to off taking channel as with more and more silting of D/S of main channel, bed level will be continuously rising.
The most general equation given by Einstein for bed load rate is as follows:
Where f* = Einstein’s bed load function.
qs = Rate or volume of sediment transported per second per unit width.
iB = Fraction of qs which is of diameter d.
ib = Proportion of grains of diameter d in the bed
d = Diameter of sediment particle
G = Specific gravity of sediment particle
g = 9.81.
For uniform soils
iB = ib and φ* = φ
Putting these values in general equation above we get following form of Einsten’s equation:
R’ is the H.M.D. which would exist in the channel with bed un-rippled. When N represents granular roughness only, Manning’s equation can be used for determining R’.
φ* – Ψ* relationship has been plotted by Einstein in form of a graph shown in Fig. 18.9. If the value of Ψ* in known φ, can be found out and so qs can be calculated from general equation given above.
For uniform bed material φ and Ψ relation can be expressed as follows:











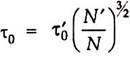
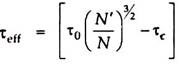
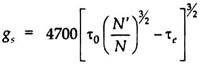







Comments are closed.