Design Principles for Gravity Retaining Walls | Soil Engineering

Gravity retaining walls derive their stability by self-weight.

The main design criteria are as follows:

i. To prevent overturning of the wall about toe.

ii. To prevent sliding of the wall at its base.

iii. To prevent tension anywhere in the base soil.

iv. To prevent bearing failure of the base soil.

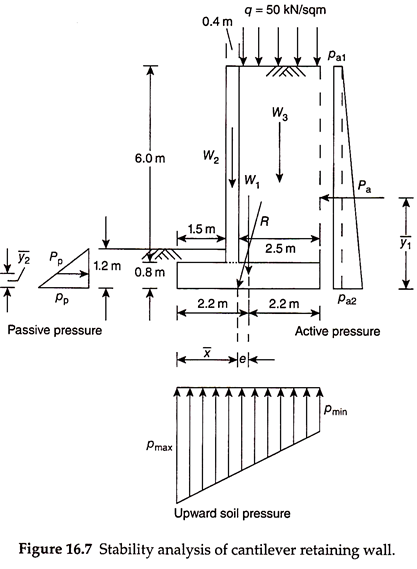
Figure 16.7 shows an example problem of the stability analysis of a cantilever retaining wall, with various forces and pressures acting as shown.

From Fig. 16.7, it is evident that the various forces/pressures acting on the wall are:

i. Active earth pressure of intensity p_a1 and p_a2 at the top and bottom of the wall, respectively.

ii. Passive earth pressure of intensity p_p at the bottom of the wall on the front side of the wall.

iii. Weight of the wall, consisting of W₁ and W₂.

iv. Weight of the backfill above the heel slab (W₃).

v. Surcharge pressure of intensity q acting on the top of the backfill.

vi. Upward soil reaction of intensity p_max below the toe and p_min below the heel of the wall.

The design principles of gravity retaining walls are discussed below:

1. Stability against Overturning:

The wall must be safe against overturning. Overturning is caused by the horizontal component of the resultant active earth pressure, P_a, in the form of an overturning moment, ΣM_o, about the toe of the wall. It is resisted by downward forces, W₁, W₂, W₃, and W₄ (due to surcharge) and the resultant passive earth pressure (P_p), in the form of a resisting moment, ΣM_R, about the toe of the wall.

Stability analysis is carried out by considering all forces per unit length (say 1 m) of the wall. P_a and P_p are cal­culated using Rankine’s theory or Coulomb’s theory. The weight of the wall is obtained as the product of the corresponding cross-sectional area (W₁ or W₂) and the density of the wall material. The weight of soil over the heel slab is calculated as the product of the cross-sectional area of the soil above the toe slab and the density of the backfill material.

The overturning moment, M_o, about the toe is computed by the following equation –

where y̅₁ is the distance of the line of action P_a above the base of the wall.

i. The resisting moment, M_R, about the toe is computed by –

where, x₁, x₂, x₃ and x₄ are the horizontal distances of W₁, W₂, W₃, and W₄, respectively, from the toe of the wall and y̅₂ is the distance of the line of action P_p above the base of the wall.

ii. The factor of safety against overturning is defined by –

The factor of safety against overturning should be generally about 2-3.

2. Stability against Sliding:

The wall tends to slide away from the backfill due to net horizontal later pressure acting on the wall. This is resisted by the frictional force between the base of the wall and the underlying soil.

i. Horizontal component of active earth pressure acting on the wall is given by –

P_aH = P_a cosα …(16.4)

where P_a is the total active earth pressure acting at an angle a with horizontal.

ii. Frictional force at the base of the wall is given by –

F_H = μΣF_y …(16.5)

iii. The factor of safety against sliding is defined by –

where μ is the coefficient of friction between the base of the slab and the underlying soil = tan ɸ.

The factor of safety against sliding should not be less than 1.5. Usually, the condition for stability against overturn­ing is automatically satisfied if the condition for stability against sliding is fulfilled.

3. Stability against Tension:

The soil reaction pressure at the base of the wall will be minimum at the heel and can be computed using –

where ΣF_y is the algebraic sum of vertical components of all forces acting on the wall, obtained from Eq. (16.8), b the width of the base slab, and e the eccentricity of the resultant force from the center of the width of the base slab, obtained from Eq. (16.9) –

Tension should not be allowed to develop at the heel, and hence, p_min should be equal to or more than zero. In other words, the eccentricity of the resultant force –

e ≤ b/6 …(16.10)

or the resultant should lie within the middle third of the base.

4. Stability against Bearing Failure:

The maximum soil reaction pressure occurs at the toe of the wall and can be determined by –

The factor of safety against bearing failure is determined using –

The factor of safety against bearing failure should not be less than 2.5.