Shear Strength Characteristics of Clays | Soil Engineering

Shear strength characteristics of clays unconsolidated undrained conditions are discussed below for normally con­solidated clays and pre-consolidated clays.

1. Normally Consolidated Clays:

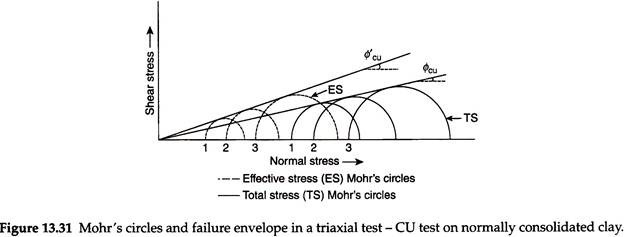
After consolidation under cell pressure is complete, no excess pore water pressure is present inside the sample. However, when the specimen is subjected to the subsequent increase of axial stress, under undrained conditions, an increase in excess pore water pressure (u) occurs. Thus, the effective stresses, σ’₁ and σ₃‘ at failure, will be less than the corresponding total stresses, σ₁ and σ₃, by the value u. But the difference σ₁ – σ₃ will be equal to σ’₁ – σ₃‘ and hence the diameters of the Mohr’s circles in terms of total stress are the same as those in terms of effective stress. The effective stress circles are shifted to the left relative to those of the respective total stress circles by a distance of u, as shown in Fig. 13.31.

It can also be seen from Fig. 13.31 that the effective angle of shearing resistance, ɸ’ (or ɸ_cu’) is greater than the apparent angle ɸ(or ɸ_cu). Furthermore, it is seen that the cohesion intercept for normally consolidated clays is zero both in the terms of total and effective stress.

2. Pre-Consolidated Clays:

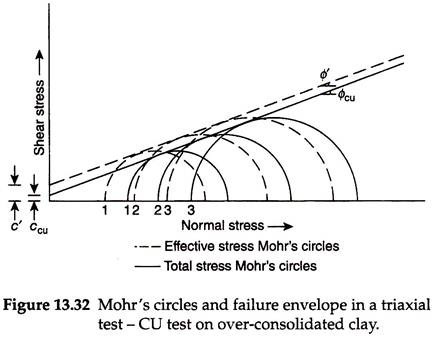
The behavior of pre-consolidated clay samples in a CU triaxial test is illustrated in Fig. 13.32. Total stress failure envelope is usually curved in the initial portion and up to the pre-consolidation pressure, after which it plots as a straight line. The failure envelope also has a cohesion intercept as shown in Fig. 13.32. The pore water pressure developed during shear will be negative up to a cell pressure equal to σ_p.

Thus, the effective stress Mohr’s circle is shifted to the right of the total stress Mohr’s circle. The true cohesion, c’, is less than the apparent cohesion, c_u. The shear strength of pre-consolidated soil up to a cell pressure of σ_p is given by –

τ = c’ + σ’ tan ɸ’ …(13.42)

At cell pressure more than σ_p, the behavior of a pre-consolidated clay would be the same as that of a normally con­solidated clay.

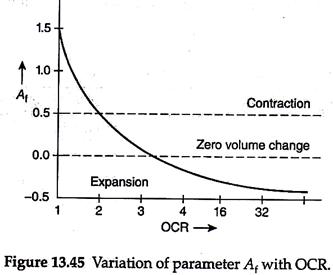
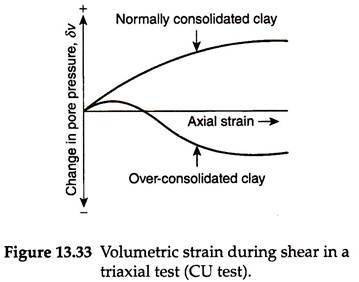
Figures 13.31 and 13.33 show the variation of Δσ (i.e., σ₁ – σ₃) and u_d with axial strain, respectively. The vari­ation of pore pressure parameter, A, defined by Eq. (13.58), with over-consolidation ratio (OCR) is also shown in Fig. 13.45. The value of A at failure (A_f) is positive for normally consolidated clays and becomes negative for over-consolidated clays. Thus, the value of A_f depends on the OCR, which is defined under triaxial conditions by –

where σ_3max is the maximum cell pressure under which the soil specimen is consolidated and σ_3R the cell pressure to which the soil specimen is allowed to rebound.

3. Use of Consolidated Undrained Strength in Engineering Practice:

The results of CU test are generally used in estimating soil strength in situations where the soil has consolidated under the pressure of foundation or under self-weight, followed by quick increase of loads causing rapid change in critical stresses without change in water content. Examples for such cases are the stability analysis of consol­idated earth dams, slopes, or other earth structures of cohesive soils under rapid drawdown. Other examples include stability analysis of foundations below consolidated clay soils for grain elevators under quick loading or unloading.

4. Unconsolidated-Undrained Test Behavior:

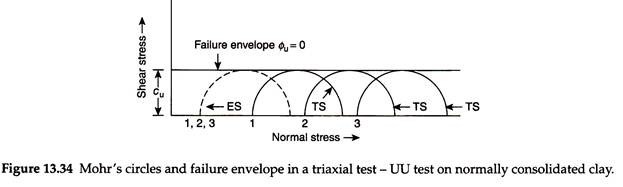
Typical results of UU test on saturated cohesive soils are shown in Fig. 13.34 for normally consolidated clay. It can be seen from this figure that the increase in cell pressure only results in equal increase in pore water pressure, since no drainage is allowed, and the subsequent increase in the total major principal stress also results in the same change in pore water pressure.

Thus, all the total stress circles and the only one corresponding effective stress circle will be of the same diame­ter. No effective failure envelope can possibly be established from this test because there is only one effective stress circle. The total stress envelope in terms of total stresses is horizontal, that is –

ɸ_U = 0 and τ = c_u = σ₁ – σ₃/2

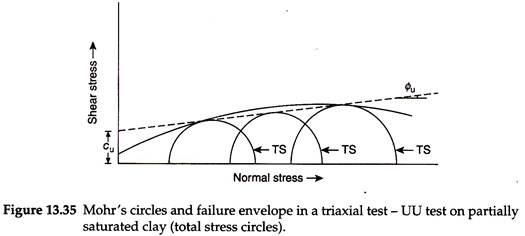
Figures 13.35 and 13.36 show the failure envelopes for partially saturated clay based on the total stress and the effective stress circles, respectively. Table 13.6 gives typical values of undrained shear strength for clays. In uniform normally consolidated clays, the undrained shear strength increases approximately linearly with depth. That is, the ratio of undrained strength, c_u, to the effective overburden pressure is approximately constant. Skempton gave the equation between the ratio (c_u/σ₀) and the plasticity index (I_p), that is –

C_u/σ₀ = 0.11 + 0.0037I_p (for I_p > 10%) …(13.44)

5. Use of Unconsolidated Undrained Shear Strength in Engineering Practice:

The results of UU strength of clays may be applied in field problems, where the critical stresses in a saturated soil mass develop too rapidly to allow any significant change in moisture content. The typical examples in saturated clays are initial bearing capacity of footings or embankment foundations, initial stability of slopes or cuts, and ini­tial stability of braced excavation.