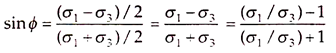ADVERTISEMENTS:
In this article we will discuss about the characteristics and factors affecting the sheer strength of sand.
Shear Strength Characteristics of Sand:
Shear strength characteristics of sandy soils depend on the drainage conditions in addition to several other parameters as discussed in the following subsections.
1. Shear Strength Characteristics of Saturated Sands during Drained Shear:
ADVERTISEMENTS:
It is nearly impossible to test undisturbed samples of cohesionless soils in either the direct shear or the triaxial compression test. Only the remolded samples are, therefore, used and the samples are to be compacted approximately to the in situ density. The direct shear test, being simpler and more rapid, is most commonly used.
The shear strength characteristics of dry and saturated sands are the same, provided the excess pore pressure is zero for saturated sands during the test. Hence, to conduct drained tests, dry sands are commonly used, as it is somewhat more difficult to test saturated sands.
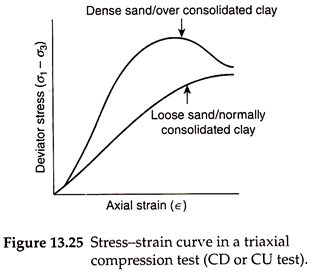
Typical curves relating principal stress difference and axial strain for dense and loose sand specimens in drained triaxial compression tests are shown in Fig. 13.25. Similar curves are obtained relating shear stress and shear displacement in direct shear tests. For dense sand, the deviator stress increases with increase in axial strain until a maximum deviator stress is reached.
After reaching the peak stress, the deviator stress decreases with further increase in the strain. For loose sand, there is no peak stress and the deviator stress increases continually with increase in axial strain. However, the rate of increase of stress per unit strain (modulus) for loose sand is less than that of dense sand. The ultimate deviator stress is approximately the same for both dense sand and loose sand.
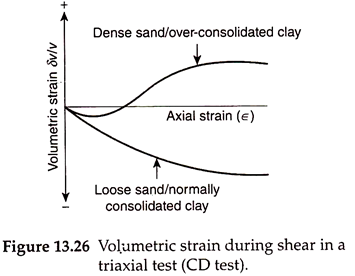
Figure 13.26 shows the volumetric strain as a function of axial strain for dense sand and loose sand. The volume of soil specimen decreases with increase in axial strain for loose sand. In case of dense sand, the volumetric strain initially decreases with increase of axial strain until the sample attains some minimum volume. The volume then increases with further increase of axial strain.
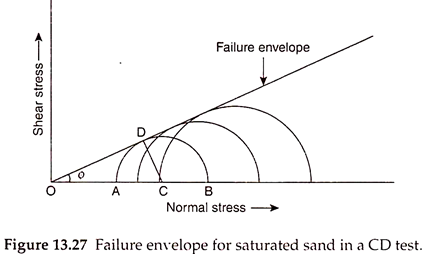
In a properly carried out drained triaxial test, a common tangent can be drawn for all the Mohr’s circles of stress as shown in Fig. 13.27. The failure plane for each of the samples makes an angle a with the horizontal as shown, which is approximately given by –
α = 45+ ɸ/2
In AOCD of Fig. 13.27, alternate expression for ɸ in terms of the principal stress ratio may be written as –
The shear strength of sands is derived basically from sliding friction between soil grains. In addition to the frictional component, the shear strength of dense sand has another component which is influenced by arrangement of soil particles. The soil grains are highly irregular in shape and have to be lifted over one another for sliding to occur. This effect is known as interlocking.
As per stress dilatancy theory, the friction angle can be expressed as –
ADVERTISEMENTS:
ɸ = ɸ u + β …(13.35)
where ɸu is the angle of sliding friction between mineral surfaces and β the friction angle due to the effect of interlocking.
In dense sand, there is a considerable degree of interlocking between particles and this interlocking must be overcome before shear failure can take place. This is in addition to the frictional resistance due to sliding between particles. The characteristic stress-strain curve for dense sand shows a peak stress at a relatively low strain and thereafter as the interlocking is overcome, the stress necessary for additional strain decreases rapidly and becomes constant with increasing strain.
The degree of interlocking will be greatest in the case of very dense, well-graded sands consisting of angular particles. As strain increases beyond the peak point on the stress-strain diagram, the interlocking stress is overcome. The ultimate shear strength (principal stress difference in the case of a triaxial test) and void ratio for dense and loose sand specimens are essentially equal under the same all-round pressure as indicated in Fig. 13.25.
ADVERTISEMENTS:
Thus, at the ultimate state, shearing takes place at constant volume, the corresponding friction angle being denoted as ɸCV‘. The reduction in the degree of interlocking produces an increase in volume of the specimen during shearing as shown in Fig. 13.26, by the relationship between the volumetric strain and axial strain.
In the case of loose sand, there is no significant particle interlocking to be overcome, because of lesser particle interference, and the principal stress difference increases gradually to an ultimate value without a prior peak.
Thus, the shear strength of loose sands is essentially due to sliding friction between soil particles. It is a function of effective normal stress at the point of contact and increases linearly with the same. The failure of loose sands at large strains may be described as progressive failure compared to the relatively sudden failure of dense sands at low strains.
Only the drained strength of sand is normally relevant in practice and typical values of the friction angle for loose sands and dense sands are given in Table 13.3. In the case of dense sands, peak value of in-plane strain can be 4° or 5° higher than the corresponding value obtained by conventional triaxial tests. This increase is negligible in the case of loose sands.
Thus, at the ultimate state, shearing takes place at constant volume, the corresponding friction angle being denoted as ɸcv‘.
2. Effect of Void Ratio and Confining Pressure on Volume Change:
The initial void ratio of the soil specimen has a significant effect on the volume change during shear. Loose sands, having high initial void ratio, tend to decrease in volume, since they do not have any interlocking effect and permit closer particle movement during shear. Dense sands with low initial void ratio have high degree of interlocking, which when overcome, produce an increase in the volume of the specimen during shear.
The effect of confining pressure is to increase the density of the soil specimen and hence reduce the void ratio. Dense sand under low confining pressure behaves similar to loose sand under high confining pressure.
3. Characteristics of Saturated Sands during Undrained Shear:
There is no advantage in using undrained test on cohesionless soils, since they tend to drain very fast in situ in most cases, as the permeability is high and the loads are applied relatively gradually.
A consolidated quick test on samples of sand may be performed in a triaxial compression apparatus, since the box shear apparatus is not suitable for this purpose. A sample of sand completely saturated is consolidated under an all-round pressure at a known initial void ratio. The sample is then sheared by keeping the drainage valve open and applying the deviator stress at a slow rate.
Typical Mohr’s circles of stress of samples subjected to c-q test are shown in Fig. 13.28. The Mohr’s failure envelope is curved at low pressure and approaches a straight line with a slope angle of ɸcq. Pore pressures are usually measured and the effective Mohr’s stress circles are drawn as shown by dashed lines. A straight Mohr-Coulomb failure envelope is obtained with a slope angle of ɸ’cq.
Factors Affecting Shear Strength of Sand:
The shear strength of cohesionless soils may be expressed by –
r = σ‘ tan ɸ …(13.36)
Factors affecting the shear strength of sands are the following:
1. Particle Size:
Gravels have higher friction angle than that of sands, which, in turn, have higher friction angle than that of silts. Larger particle size promotes better degree of interlocking of particles in soils of same density, leading to higher friction angle.
2. Particle Shape:
Crushed gravel and sand with angular particles have higher friction angle due to better degree of interlocking than the bank run gravel and sand with rounded particles.
3. Gradation:
Well-graded soils can be compacted to higher density, leading to better degree of interlocking and higher friction angle than that of poorly graded soils.
4. Initial Void Ratio During Shear:
Dense sands, with lower initial void ratio during shear, give a higher friction angle from peak stress compared to the friction angle of loose sands of higher initial void ratio. Loose sands with initial void ratio more than critical void ratio (CVR) are susceptible to liquefaction under suddenly applied loads due to loss of shear strength. Dense sands with initial void ratio less than CVR are not susceptible to liquefaction.
5. Cementation:
Naturally occurring cementation between particles give higher shear strength to the soils.
6. Type of Minerals:
If sand contains mica, it will have higher void ratio and hence less shear strength. However, the friction angle is same for soils containing quartz or feldspar minerals.
7. Pore Water Pressure:
A positive pore water pressure reduces the effective stress and decreases the shear strength. Negative pore water pressure, due to capillary tension in partially saturated sands, increases the effective stress and shear strength temporarily.
8. Seepage:
Seepage of water, occurring in downward direction, increases the effective stress and shear strength, whereas when it occurs in upward direction, it reduces the effective stress and causes quick condition due to loss of shear strength.
9. Dynamic Loads:
Suddenly applied dynamic loads, such as earthquakes or pile-driving or other construction operations, develop positive excess pore pressures in loose sands and reduce the effective stress causing liquefaction due to loss of shear strength.
10. Intermediate Principal Stress:
Soils in plane strain condition, that is, where strain in one direction is zero, have higher friction angle than that in the triaxial condition, where intermediate principal stress is present. This shows that the effect of intermediate principal stress is to decrease the friction angle.
11. Deviator Stress:
High values of deviator stress decreases the effective friction angle, ɸ’, due to crushing of sand grains. In practice, however, such higher deviator stresses are seldom experienced by soil deposits as to cause the crushing of the soils grains.
12. Confining pressure:
Increasing confining or consolidation pressure decreases ɸ’, although the shear strength increases. In other words, increase of confining pressure increases shear strength but decreases the rate of increase of shear strength.
13. Type of Shear Test:
Direct shear tests more closely resemble plane strain condition and hence may give higher friction angle for the same soil than that by the triaxial test. In situ tests may give higher friction angle due to naturally occurring cementation.
14. Drainage Condition:
Undrained tests (CC and CU) give lower friction angle than the drained (CD) tests for the same soil.
15. Sample Disturbance:
Sample disturbance causes loss of natural cementation and original soil structure giving a lower friction angles than that in undisturbed condition for the same soil.
16. Repeated loading:
A cyclic stress much smaller than static failure stress may cause very large strains and hence failure of the soil.