ADVERTISEMENTS:
The stability of slopes of earth dams is checked under the following conditions: 1. Downstream under Steady Seepage 2. Determination of Pore Pressure at the Bottom of each Slice 3. Upstream Slope under Sudden Drawdown 4. Upstream and d/s Slopes during and Immediately after Construction.
1. Stability of Downstream Slope under Steady Seepage:
When the reservoir on the u/s side of the earth dam is filled, water starts seeping through body of the dam. After some time, steady seepage conditions are established and a well-defined phreatic line is formed. The soil below the phreatic line is saturated and is subjected to seepage pressure.
The seepage forces are directed inward into the body of the dam on the u/s side and hence increases the stability of the u/s slope. However, on the d/s side, the seepage forces are directed outward and hence aid the gravity forces in decreasing the stability of the d/s slope. The steady seepage condition is therefore critical for the d/s slope of the earth dam.
ADVERTISEMENTS:
The factor of safety of the d/s slope under steady seepage is determined for a trial slip surface using the method of slices. The wedge of soil in the d/s slope above the trial slip surface is divided into a number of slices of equal width.
The weight of each slice is computed by considering the bulk density of soil above the phreatic line and saturated density below the phreatic line. The weight of each slice is resolved into normal (Ni) and tangential (Ti) components about a line tangential to the mid-point of each slice at its bottom. Driving moment will be –
where r is the radius of trial slip surface. The resisting moment will be –
where S is the total shear strength at the bottom of each slice.
The shear strength at the bottom of each slice is calculated from the relation –
However, for the slices that are intersected by the phreatic line, only effective normal component Ni ‘ must be used in determining the shear strength by subtracting the total pore pressure (u × Δl) at the bottom of the slice from the corresponding total normal component, Ni Thus, the total shear strength of the soil along the trial slip surface is given by –
The analysis is repeated for a large number of trial slip surfaces and corresponding factors of safety are determined. The minimum factor of safety so obtained is taken as the factor of safety of the d/s slope during steady seepage and the corresponding trial slip surface is the critical slip surface.
2. Determination of Pore Pressure at the Bottom of each Slice:
The determination of factor of safety during steady seepage condition requires the knowledge of pore water pressure distribution along different trial slip surfaces. The pore pressure distribution is determined with the help of the flow net.
Figure 17.14 shows the flow net for the earth dam. The first equipotential line (EPL1) intersects the phreatic line at point a and the trial slip surface at point b. The pore pressure u2 at point b is equal to the vertical distance between points a and b to the scale of the flow net or the dam section.
This pore pressure is plotted normal to a tangent drawn at point b on the slip surface. The second equipotential line intersects the phreatic line and the slip surface at points c and d, respectively. The pore pressure u2 at point d is equal to the vertical distance between points c and d and is plotted at point d normal to tangent at d.
ADVERTISEMENTS:
Thus, the pore pressure distribution at different points is determined in this way and the extremities of these normal lines are joined by a smooth curve that represents the pore pressure distribution along the slip surface below phreatic line. The pore pressure ui at the center of the bottom of each slice can be determined from this curve, by drawing a normal from the mid-point of the bottom of the slice.
3. Stability of Upstream Slope under Rapid (Sudden) Drawdown:
The critical condition for the stability of u/s slope of an earth dam occurs when there is rapid drawdown from the u/s side of the reservoir. If the soil is of low permeability, no appreciable change in the water level inside the body of the dam takes place when the reservoir level goes down.
The weight of water, which is still present in the soil slope, tends to cause sliding of the wedge as the water pressure, which was acting on the u/s slope to balance this weight, has been suddenly removed. From another view point, the shear strength of the soil is considerably reduced due to pore pressure developed in the soil; whereas the destabilizing force due to the saturated weight of soil remains the same.
ADVERTISEMENTS:
The flow net for the sudden drawdown condition can be drawn using the electrical analogy method, and the pore pressure acting on the base of the various slices is determined. The stability of the u/s slope during sudden drawdown is determined using the relation –
A more convenient method consists of estimating the pore pressure (u) using Skempton’s pore pressure parameters. Figure 17.15 shows the u/s slope of the dam. The pore water pressure at any point P before drawdown is given by –
where h is the height of soil above point P, hw is the height of water above the point P, and h’ is the loss of head due to seepage from upstream slope up to (EPL through) point P, as shown in Fig. 17.15.
Major principal stress at point P, σ1 is equal to the weight of soil and water above point P. When there is a drawdown, the major principal stress at point P decreases by –
and the change in the pore water pressure at point P is given by –
where B̅ is the overall pore pressure coefficient given by –
Hence the pore pressure at point P, immediately after the drawdown is given by –
The value of B̅ is slightly greater than unity. A conservative value of B equal to unity is generally taken. Thus –
The factor of safety is obtained from Eq. (17.24) using the pore pressure computed from Eq. (17.27).
An approximate alternative method for stability analysis of u/s slope under sudden drawdown is to consider the saturated unit weight of soil for calculating driving forces (IT,) and submerged unit weight for calculating the resisting forces (ΣTi) in Eq. (17.24). Thus –
As the water pressure on the slope is still acting below the drawdown level, the submerged unit weight is used both for driving forces and for resisting forces.
If the slope material has high permeability, it drains as fast as the reservoir level goes down, then the driving and resisting forces are calculated using bulk unit weight.
If the slope material is of medium permeability, the saturation line moves down at a rate depending on the permeability of the soil. A series of flow nets can be drawn for different positions of saturation line and the corresponding pore pressure is determined and the factor of safety is estimated.
4. Stability of u/s or d/s Slope During Construction:
An embankment or earth dam is normally compacted at 80%-90% saturation. When the embankment soil is of low permeability, excess pore pressure develops due to compaction during construction or due to its own weight. The pore pressures developed depend on the placement water content, method of compaction, weight of the overlying soil, permeability of the soil, and rate of construction. The prediction of pore pressure during the design stage is rather difficult.
The stability analysis of the u/s slope and d/s slope during construction are carried out by the method of slices. The analysis involves computation of driving moment that is due to tangential component of weight of the slices, and the resisting moment that is due to shear strength of the soil along the trial slip surface.
The determination of the shear strength along the trial slip surface, and hence the resisting moment, requires the knowledge of pore pressure during construction. Hilf has given a method to estimate pore pressure during construction based on laboratory test results as shown by the following relation –
where u is induced pore air pressure, po is the pore air pressure before compaction (atmospheric pressure) Δ is the embankment compression as a percentage of embankment volume, Va is the volume of free air in soil pores after initial compaction, Vw is the volume of water present in unit volume of embankment soil, and h is Henry’s constant of solubility of air in water by volume ≈ 0.02 at 20°C
When Δ = Va, the entire air goes into the solution and the soil becomes saturated. The pore pressure is then given by –
A graph is plotted between the effective stress σ’ and the percent consolidation Δ, as obtained from the consolidation tests conducted on the samples in the laboratory. The values of pore pressure are calculated using Eq. (17.29) for different values of Δ. The total stress is calculated from the following equation –
σ = σ̅ +u……. (17.31)
A plot is then made between the total stress and the pore pressure u. The plot is used for the determination of pore pressures at various points on the dam during construction. The total stress is obviously equal to the bulk unit weight multiplied by the depth of the soil above.

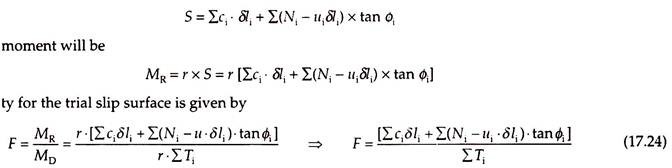






Comments are closed.