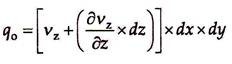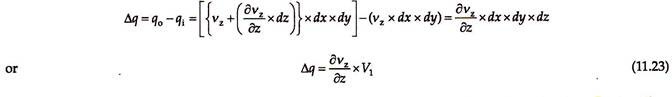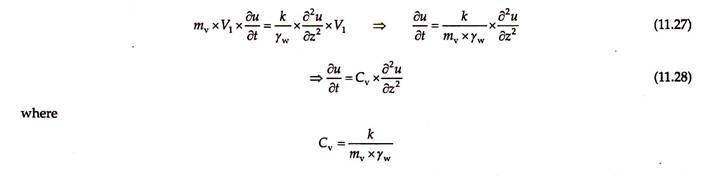Terzaghi’s Theory of Consolidation | Soil Engineering

In this article we will discuss about:- 1. Introduction to Terzaghi’s Theory of Consilidation 2. Assumptions in Terzaghi’s Theory of Consolidation 3. Validity of Terzaghi’s Theory 4. Solution of Consolidation Equation.

Introduction to Terzaghi’s Theory of Consilidation:

The total consolidation settlement  is time dependent. It is often necessary to determine – i. Settlement that occurs in a given time after the construction of the structure. ii. Time taken for a given settlement to occur. Terzaghi developed the theory of consolidation that makes these time-settlement computations possible.

This is explained below:

1. Velocity of Pore Water:

Let u be the excess pore pressure developed at any instant of time during consolidation. Then, the head causing flow during the expulsion of pore water from the stressed zone of the soil is –

h = u/γ_w …(11.20)

Assuming that the flow of water during expulsion of pore water occurs only in the vertical direction, hydraulic gradient is given by –

i = ∂h/∂z

Substituting the value of h from Eq. (11.20) we get –

i = ∂/∂z (u/γ_w)

Since the density of pore water, γ_w, is uniform, assuming homogeneous condition we have –

i = 1/γ_w (∂/∂z) …(11.21)

As per Darcy’s law, velocity of flow of pore water v_z = k x i. Substituting the value of i from Eq. (11.21) we get –

Assuming that the soil is homogeneous, permeability will be uniform. So –

2. Flow Rate of Pore Water:

Consider the flow that is taking place through a small soil element of dimensions dx, dy, and dz in x, y, and z coordinate directions, respectively, as shown in Fig. 11.17.

Let v_z be the velocity of pore water entering the soil element. Velocity of pore water leaving the soil element is –

v_o = v_z +(∂v_z/∂z) × dz

We know that the rate of flow (i.e., volume per unit time) of pore water is given by q = v × A, where v is the velocity of flow and A is the area of flow. Hence, volume of water entering the soil element per unit time is –

q_i = v_z × dx × dy

Volume of water leaving the soil element per unit time is –

Volume of pore water squeezed (expelled) out of the element per unit time is –

where V₁ is the initial volume that is equal to dx × dy × dz. Substituting the value of (∂v_z/∂z) from Eq. (11.22) in Eq. (11.23), we have –

3. Change in the Volume of Soil Due to Consolidation:

From the definition of the coefficient of volume compressibility given by Eq. (11.8), we have –

m_v = (–ΔV/V₁) × (1/Δσ’)

Change in the volume of soil is –

ΔV = –m_v × V₁ × Δσ’

Change in volume per unit time is given as –

∂/∂t (ΔV) = ∂/∂t (–m_v × V₁ × Δσ’)

Assuming that (a) the coefficient of volume compressibility, m_v, remains constant with time and that (b) the change in the volume of soil due to consolidation is negligible, we have –

∂/∂t (ΔV) = –m_v × V₁ × ∂/∂t (Δσ’) …(11.25)

From Terzaghi’s effective stress principle, we have –

Δσ = Δσ’ + u

Differentiating both sides with respect to time, we have –

∂/∂t Δσ = ∂/∂t Δσ’ + ∂u/∂t

As the total stress, Δσ, is constant with time during the consolidation, that is –

∂/∂t Δσ = 0

we have –

Substituting this value in Eq. (11.25), we have –

As the change in the volume of soil is only due to expulsion of pore water,

∂/∂t (ΔV) = Δq

Hence, equating Eqs. (11.26) and (11.24), we have –

C_v is known as the coefficient of consolidation. Its units are m²/s or cm²/s. It indicates the speed with which con­solidation takes place. Higher the value of coefficient of consolidation, faster will be the rate of consolidation and less time will be required to complete the consolidation. Equation (11.27) is Terzaghi’s one-dimensional (1D) con­solidation equation.

Assumptions in Terzaghi’s Theory of Consolidation:

Summarizing the assumptions made in the derivation of Terzaghi’s consolidation equation, we have the following points:

1. The soil is homogeneous and fully saturated.

2. Soil particles and pore water are incompressible.

3. The flow of water during expulsion of pore water occurs only in the vertical direction, that is, consolidation is one-dimensional (1D).

4. The change in the volume of soil due to consolidation is negligible compared to the initial volume of soil.

5. Flow is laminar and Darcy’s law is valid.

6. Permeability is the same throughout the thickness of the compressible soil layer.

7. The coefficient of volume compressibility, m_v, remains constant with time.

8. Compression takes place only due to expulsion of pore water, that is, the initial and secondary consolidation is neglected.

9. The coefficient of consolidation for a given soil and site conditions is assumed to be constant.

Validity of Terzaghi’s Theory:

The validity of the assumptions made in Terzaghi’s theory of one-dimensional consolidation is discussed as follows:

1. Assumptions 1, 2, and 4 are reasonable and valid for most practical situations.

2. Consolidation is generally three-dimensional (3D) in the field. The theory has been later extended to include the effect of 3D consolidation.

3. Assumption 5 is valid for most fine-grained soils where the hydraulic gradients are sufficiently high.

4. Assumption 6 may be also valid for most practical cases where the clay layer is homogeneous.

5. Coefficient of volume compressibility is found to vary with variation in effective stress.

6. Assumption 8 is valid for most inorganic clays of medium compressibility. With increased presence of sand or silt in a soil, the initial consolidation may be more. For highly organic soils and fat clays, secondary consolidation forms a significant portion of the total settlement and has to be taken into consideration.

7. In practice, it was observed that C_v varies with change in effective stress. For accurate determination of time rate of settlements, C_v should be determined from the consolidation test for a wide range of pressure expected in the field and the value for the required pressure range should be used while making time-settlement computations.

Solution of Consolidation Equation:

The one-dimensional consolidation equation, Eq. (11.27), given by Terzaghi is a partial differential equation of second order. Its solution can be obtained by Fourier series. It is evident from the equation that the excess pore water pressure (u) is a function of depth (z) and time (t). It may be represented by the following equation –

u = f₁(z) × f₂(f)

Substituting the value of u in Eq. (11.27) and solving using the Fourier transforms, we have –

Equation (11.29) consists of the following three non-dimensional factors:

1. Degree of Consolidation (U):

The degree of consolidation, also known as consolidation ratio, indicates the progress of consolidation at any time at the given location z in the compressible layer. The degree of consolidation (U) at any time during consolidation is defined as the percentage of compression that has been completed at that time relative to the total consolidation settlement under the given effective stress increment. It is usually expressed in percentage.

U = (ρ/ρ_f) × 100 …(11.30)

where ρ is the compression (decrease in the thickness of soil due to consolidation) at any given time and p_f is the final settlement at the end of consolidation given by Eq. (11.14) through Eq. (11.17).

As the compression essentially depends on the dissipation of pore water pressure, the degree of consolida­tion (U) is also defined as the percentage pore water pressure (u_d) dissipated at any time to the total pore water pressure (u) to be dissipated for completion of consolidation –

U = (u_d/u) × 100 …(11.31)

Evidently, u the total pore water pressure to be dissipated = Δσ = applied stress increment.

2. Drainage path Ratio (Z):

It is defined as –

Z = z/d

where z is the distance from the drainage face and d is the longest distance the pore water has to travel for drain­age. It is equal to the thickness of the compressible layer if a pervious stratum is present only on one side (top or bottom) of the compressible layer. It is equal to half the thickness of the compressible layer if a pervious stratum is present on top and bottom of the compressible layer.

Thus, if a pervious soil (drainage face) layer is available only on one side (top or bottom) of the compressible layer, that is, for single drainage –

d = H …(11.32)

If pervious soil (drainage face) layer is available on both top and bottom of the compressible layer, that is, for double drainage –

d = H/2 …(11.33)

where H is the thickness of the compressible soil layer undergoing consolidation.

3. Time Factor (T):

It is defined as –

T = (C_v × t)/d₂ …(11.34)

where t is the time corresponding to a given degree of consolidation, C_v the coefficient of consolidation, which is a property of soil and can be determined from a laboratory consolidation test (its units is cm²/s), and d the length of the drainage path. For a given compressible layer, where C_v and d are constant, the time factor is directly pro­portional to the time elapsed. The time factor is a function of the degree of consolidation, U. It is given by Eqs. (11.32) and (11.33).

The following boundary conditions are used for solving Terzaghi’s ID consolidation equation:

i. At time t = 0, u = u_i at all locations, that is, for all values of z.

ii. At time t = ∞, u = 0, for all values of z.

iii. At time t > 0, u = 0, when z = 0.

iv. At time t > 0, u = 0, when z = 2d (for single drainage condition) and z = d (for double drainage condition).

The solution of Terzaghi’s 1D consolidation equation consists of equations relating the three non-dimensional parameters T, U, and d.

While the relation between T and d is given by Eq. (11.34), the relations between T and U are given by the following equations:

T = (π /4U²) if U < 60% …(11.35)

T = –0.9332log₁₀ (1 – U) – 0.0851 if U > 60% …(11.36)