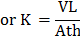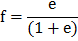Assessment of Wind Erosion | Soil Management

The assessment of wind erosion requires a precise knowledge on erosive force of wind, which mainly depends on wind velocity or in other words, the energy of wind. From wind energy, the wind erosivity is determined. The wind erosivity is the ability of wind to erode the soil.

The kinetic energy of wind is deter­mined with the help of meteorological parameters from which the average wind velocity for a particular frequency of occurrence is determined. The average wind velocity is then applied for computing the kinetic energy of wind, for which the following formula can be used –

W_k = 2.25 V²_0.2 … (7.47)

In which, W_k is the kinetic energy of wind with 0.2 frequency of occurrence and V_0.2 is the wind velocity for 0.2 frequency of occurrence (m/s). The kinetic energy computed so, is expressed in the unit of MJ/ha/h.

For assessment of wind erosion, an equation similar to Universal Soil Loss Equation has been developed by Woodruff and Siddoway (1965), taking into account of soil erodibility (I), wind energy expressed by a factor called climatic factor (C), surface roughness factor (K), length of open wind blow factor (L) and vegetative cover factor (V).

The equation is given as under:

W.E. = f (I, C, K, L, V) … (7.48)

In which, WE is the annual wind erosion (t/ha), I is expressed as t/ha/year, L is in m, V in kg/ha and C ԑ’ K are dimensionless. This equation considers all those principal factors, which influence the soil erosion, caused by wind force.

The equation involves interactions between the factors, therefore, it cannot be solved by multiplying the values of different factors, together. The factor relationships are rather complex and their prediction can only be obtained by using either complicated charts/nomographs or equations, developed for them.

Different factors associated with the equation are described as under:

1. Soil Erodibility Factor (I):

It describes the potential annual soil loss in mt/ha from a wide, level, unsheltered, isolated bare field and non-crusted soil surface. The values of soil erodibility factor (I) have been determined from wind tunnel studies, in the field near Garden City Kansas during 1954 to 1956. The determination of ‘I’ was carried out by measuring the depth of soil removed during individual wind storm and extended over the windy spring months, each year.

The estimated values of ‘I’ are appended in Table 7.10. These values are modified for the slope greater than 1.5% and slope length less than 150 m, called knolly topography, because wind is more erosive over the top of knolls. This type of adjustment is referred by the term ‘Is’, which gives the relationship between soil erodibility on a particular slope and erodibility on level land.

2. Climatic Factor (C):

This factor is determined by accounting the wind velocity and soil moisture content, because climate directly affects these two components very rapidly, and thereby the wind erosion, too. The wind velocity has great effect on detaching of the soil particles from the soil surface.

The detaching power of wind varies as the square of velocity and transporting power as fifth power of the velocity. Chepil etal (1962) reported that, the rate of soil movement varies as the cube of wind velocity and inversely as the square of surface soil moisture content, as presented below –

In which, C is the climatic factor, u is the wind velocity (mean annual) measured at the height of 9 m from the ground surface and (p – E) is an index called Thornthwait (p – E) index.

The following equation can be used for computing the (p – E) index:

Where,

P = mean precipitation for the month i (in)

T = mean temperature for the month i (°F); a minimum value as 18.4 is used for (T – 10)

In above equation, Thornthwait did not use the recorded temperature data of the months with very low temperature, rather he used 28.4°F as the minimum mean monthly temperature. A modification is also essential for higher latitudes, where majority of the months have the temperature considerably below the freezing, each year.

Chepil reported that, in extremely dry regions the (p – E) is not a satisfactory index to accommodate the effect of soil moisture on wind erosion, because the equation 7.50 translates an extremely large value, where magnitude of monthly precipitation is very low. He quoted that in U.S.A. at some locations, this equation yields the values of C as high as 1000, which resulted the amount of wind erosion very high than the ever measured.

3. Surface Roughness Factor (K):

It is also known as soil-ridge roughness factor.

The surface roughness is mainly resulted from the following three elements:

i. Cloddiness of the surface soil

ii. Vegetative cover; and

iii. Ridges on the soil surface.

The effect of cloddiness of soil surface on wind erosion has been considered in the soil erodibility factor (I) and the effect of vegetative cover is accounted in vegetative factor (V). The effect of surface roughness caused by ridges on wind erosion is counted as the soil-ridge roughness factor (K).

4. Ridge Roughness (R):

It is defined as the height of ridge composed of non-erodible gravels of 2.0 to 6.4 mm in size with height-to-spacing ratio as 1:4 that affects the erosive power of wind in the same way as field ridges. For example, if 12 cm gravel ridges are there at 48 cm interval perpendicular to the wind direction to check the wind velocity, then ridge-roughness coefficient would be 12 cm for the field.

Chepil devised a method to predict the ridge roughness (R) from the measured roughness of field, which involves following relationship:

R = [Measured field ratio (1:x)/Standard ratio (1:4)] x Measured ridge height

The measured field ratio (1:x) is determined by measuring the ridge height and spacing between them.

Once, the value of ridge-roughness equivalent (R) is determined, the surface-roughness factor (K) is computed by using the Fig 7.18, developed by Woodruff and Siddoway (1965).

Morgan (1986) have also reported another approach to determine the ridge-roughness factor (K), explained in the following steps:

(1) Compute the value of ridge roughness (R) by the following equation –

R = H²/I … (7.51)

In which, H is the height of ridge (mm) and I is the distance between the ridges, formed. This relationship is valid for those fields, in which surface roughness has been caused by the tillage and planting equipments.

(2) Alter determining the ridge roughness (R) using above equation calculate the ridge roughness factor (K) as under –

K = I for R < 2.27

K = 1.125 – 0.153 In R for 2.27 ≤ R < 89

K = 0.336. exp (0.00324 R) for R ≥ 89.

5. Length of Open Wind Blow (L):

Sometimes, it is also nomenclatured as width of field factor.

The following parameters are required for determining the length of open wind blow or width of field factor:

(a) Preponderance of Erosive Force (R_m):

It is obtained by determining the product of cube of the mean wind speed and the duration factor for all wind speed groups, separately, for each sixteen compass directions, and to all them adding together. By vector analysis the value of R_m is also determined, which is done by calculating the forces acting parallel and perpendicular to the prevailing direction in ratio form, given as under –

R_m = Σ Wind erosion forces acting parallel/Σ Wind erosion forces acting perpendicular

The value of R_m is taken as 1.0, when there is no prevailing wind-erosion direction, and R_m as 2.0 for the situation when prevailing wind-erosion and erosion forces acting parallel to prevailing wind, are twice as large as those acting perpendicular. The essential data required for above calculations, can be obtained from the local soil conservation/ meteorological centres.

(b) Deviation of the direction of prevailing wind erosion forces from perpendicular to the field or field strip border (A)

(c) Median Field Width Factor (K₅₀):

It is a median condition in which half of the erosive winds travel farther and half not as the prevailing wind direction across the field. It can be directly obtained from the Table 7.11, given by USDA-Soil Conservation Service. The K₅₀ obtained from the table, is for the given values of R_m and A. After determining the value of K₅₀, the width of field factor (L) can be computed by the following relationship –

L = D₅₀ – 10.B … (7.52)

In which, D₅₀ is the product of K₅₀ and dimension of the field and B is the height of barrier. The term 10 B is called sheltered distance.

Morgan (1986) described another method for computing the ‘L’, which involves the computation of L as the function of field length (l), field width (w), field orientation expressed as the clock-wise angle between field length and north (ɸ) and wind direction as clock-wise from the north (α). The formula used for computation is given as under –

This equation provides L value in the unit of m, if I and w are in m and α and ɸ are in radian.

The estimation of effect of width of field factor (L) on soil loss, is very complex as it depends on the magnitude of soil, carried by the wind. How­ever, a nomograph has been developed to predict the effect of L on wind erosion by incorporating the soil erodibility-soil-ridge-roughness erosion esti­mates (E₂) and soil-erodibility-soil-ridge rough­ness-climatic-erosion estimates (E₃). The nomo­graph is shown in Fig. 7.19, reported by Woodruff and Siddoway (1965).

The computation of soil loss E₄ = f(l K C L), using the nomograph is described under following steps:

Step (1) – The nomograph is developed show­ing the relationship among soil loss E₂ = f(l, K), E₃ = f(I, K, C) and unsheltered distance across the field. For determining the soil loss E₄ = f(l, K, C, L), arrange the data on E₂, E₃ and unsheltered distance.

Step (2) – Place the scale along left side of the graph, in such a way that E₃ on the scale is aligned with E₂ on the graph.

Step (3) – Draw a parallel line to the line to its intersection with the axis of unsheltered distance for the given value of E₃.

Step (4) – Draw a horizontal line from the intersection point, back to the movable scale. The point at which it cuts the movable scale, is the value of E₄.

6. Vegetative Cover Factor (V):

The effect of vegetative cover on soil erosion due to wind action is because of its various features, such as amount of dry matters it contains, standing live biomass, relative texture, height when standing and whether it is living or dead, standing or flattened.

Since, the original work for evaluating the effect of vegetation on soil loss was done for the flattened wheat straw, therefore the vegetative factor (V) in erosion equation is required to modify for flattened wheat straw equivalents (R’). Woodruff and Siddoway (1965) have developed different curves for modifying the effect of different types of vegetative cover in terms of equivalents of flattened wheat straw (R’), as –

1. Curves to convert the weights of living or dead small grain from seedling or stooling stages (R’) into equivalent amounts of flattened wheat straw (V).

2. Curves to convert the weights of small grain stubble (R’) into equivalent amounts of flattened wheal straw (V).

3. Curves to convert the weights of sorghum stubble (R’) into equivalent amounts of flattened wheat straw (V).

As per existing vegetative cover, the equivalent (R’) for flattened wheat straw is determined, which is substituted in the soil loss predicting equation.

Woodruff and Siddoway (1965) have also derived a set of curves for determining the soil loss E = f(l, K, C, L, V) for the given value of vegetative factor (V) and E₄ = f(l, K, C, L). The curves are shown in Fig. 7.20.

Lyles and Allison (1981) have also developed the relationship for predicting the flattened wheat-straw or small grain equivalent weight of residues (SGe), given as under –

Where,

R_w = weight of standing crop residues (kg/ha)

d = average stalk diameter (cm)

r = average specific weight of the stalks (mg/m³)

The above equation is valid for wide range of crops. The determined value of equivalent weight of residues is substituted in the equation for estimating the soil loss, caused by wind erosion.